Step-by-step explanation:
Let
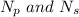 are the number of turns in primary and secondary coil of the transformer such that,
are the number of turns in primary and secondary coil of the transformer such that,
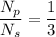
A resistor R connected to the secondary dissipates a power
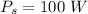
For a transformer,
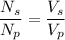
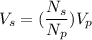
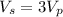 ...............(1)
...............(1)
The power dissipated through the secondary coil is :
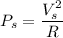
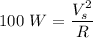
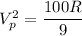 .............(2)
.............(2)
Let
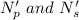 are the new number of turns in primary and secondary coil of the transformer such that,
are the new number of turns in primary and secondary coil of the transformer such that,
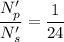
New voltage is :
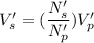
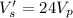 ...............(3)
...............(3)
So, new power dissipated is
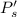
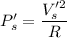
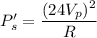
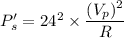
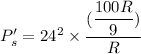
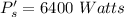
So, the new power dissipated by the same resistor is 6400 watts. Hence, this is the required solution.