Question

Running at their respective constant rates, Machine X takes 2 days longer to produce w widgets than Machine Y. At these rates, if the two machines together produce 54w widgets in 3 days, how many days would it take Machine X alone to produce 2w widgets?

Answer 1

12 days.

Explanation:

`\because Efficiency = (Work)/(Time)`

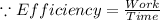
Let x be the time taken by machine Y to produce w widget,

So, the efficiency of machine Y =
`(w)/(x)`,

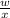Since, X takes 2 days longer to produce w widgets than Machine Y,

So, the efficiency of machine X =
`(w)/(x+2)`,

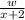If total work =
`(5)/(4)w`,

Then the time taken by machines X and Y when they work together

`=\frac{5/4w}{\text{efficiency of machine A}+\text{efficiency of machine B}}`

`=(5w)/(4((w)/(x+2)+(w)/(x)))`

`=(5)/(4((x+x+2)/(x(x+2))))`

`=(5x(x+2))/(8x+8)`

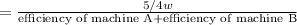
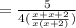
According to the question,

`(5x(x+2))/(8x+8)=3`

`5x^2+10x = 24x+24`

`5x^2-14x-24=0`

`5x^2-20x+6x-24=0`

`5x(x-4)+6(x-4)=0`

`(5x+6)(x-4)=0`

`\implies 5x+6=0\text{ or }x-4=0`

`\implies x=-(6)/(5)\text{ or }x=4`

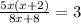
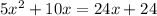
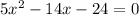
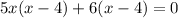
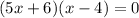
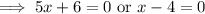
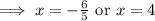
Number of days can not be negative,

Hence, the time taken by machine X to produce w widgets = x + 2 = 4 + 2 = 6 days,

Therefore the time taken by machine X to produced 2w widgets would be 12 days.