Question

Tiffany is constructing a fence around a rectangular tennis court. She must use exactly 300 feet of fencing. The fence must enclose all four sides of the court. Regulation states that the length of the fence enclosure must be at least 80 feet and the width must be at least 40 feet. Tiffany wants the area enclosed by the fence to be as large as possible in order to accommodate benches and storage space. What is the optimal area, in square feet?

Answer 1

5600 square feet is the area.

Explanation:

Perimeter will be = 300 feet

Length of the fence enclosure must be at least 80 feet.

Width of the fence enclosure must be at least 40 feet.

Let x be the length and y be the width of the court.

We get following constraints:

`x \geq 80`

`y \geq 40`

If we calculate the area, we get
`xy \geq3200`

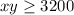
And for the perimeter we get:
`2x+2y=300`

⇒
`x+y= 150`

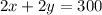
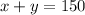
Now look at the graph attached, we get point (80,70) as the possible solution.

So, the maximum area occurs when the dimensions are 80 feet by 70 feet.