Answer:All balls have same velocity
Step-by-step explanation:
Ball A
horizontal velocity

vertical velocity
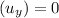
let h be the height of building
Vertical velocity acquired by Ball A
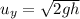
Velocity just before hitting ground=
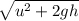
Ball B
launched with velocity u at angle of 45 above horizontal
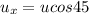
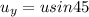
horizontal velocity will remain same as there is no acceleration in that direction
vertical velocity just before hitting the floor
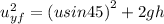
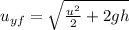
Final velocity before hitting ground
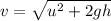
Ball C
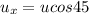

horizontal velocity will remain same as there is no acceleration in that direction
vertical velocity just before hitting the floor

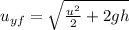
Final velocity before hitting ground
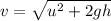
Thus all three balls will have same final velocity.