Question

The overall distance traveled by a golf ball is tested by hitting the ball with Iron Byron, a mechanical golfer with a swing that is said to emulate the legendary champion, Byron Nelson. Ten randomly selected balls of two brands are tested and the overall distance measured. Assume that the variances are equal. The data follow: Brand 1: 277 278 287 271 283 271 279 275 263 267 Brand 2: 262 248 260 265 273 281 271 270 263 268 Is there evidence to show that there is a difference in the mean overall distance of brands?

Answer 1

The tabulated value is less than the calculated value, therefore we accept the null hypothesis and It show that there is a difference in the mean overall distance of brands.

Explanation:

The given data sets are

Brand 1: 277 278 287 271 283 271 279 275 263 267

Brand 2: 262 248 260 265 273 281 271 270 263

We need to check that whether there is a difference in the mean overall distance of brands or not.

`\overline{x}_1=275.1`

`\overline{x}_2=265.89`

`s_1=7.2793`

`s_2=9.3601`

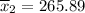
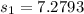
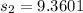
Null hypothesis:

`H_0:\mu_1=\mu_2`

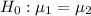
Alternative hypothesis:

`H_a:\mu_1\\eq \mu_2`

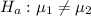
The data is normally distributed, we assume that the variances are equal so we will apply t-test.

The formula for t-statistics is

`t=\frac{(\overline{x}_1-\overline{x}_2)-(\mu_1-\mu_2)}{s\sqrt{(1)/(n_1)+(1)/(n_2)}}`

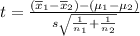
where,

`s=\sqrt{((n_1-1)s_1^2+(n_2-1)s_2^2)/(n_1+n_2-2)}`

`s=\sqrt{((9)(7.2793)^2+(9)(9.3601)^2)/(10+10-2)}`

`s=8.3845`

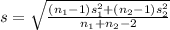
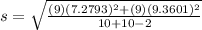
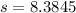
The value of t is

`t=\frac{(265.89-275.1)-(0)}{8.3845\sqrt{(1)/(10)+(1)/(10)}}`

`t=-2.456`

`|t|=2.456`

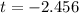
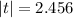
Degree of freedom is

`d.f.=10+10-2`

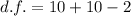
From t-table the t-value for 0.05 level of significance at 18 degree of freedom is ±2.1009.

Since the tabulated value is less than the calculated value, therefore we accept the null hypothesis and It show that there is a difference in the mean overall distance of brands.