Given:
Pressure,
 = 1300 kPa
= 1300 kPa
Temperature,
 =
=
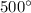
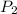 = 100 kPa
= 100 kPa
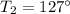
velocity, v = 40 m/s
A = 1

Solution:
For air propertiess at
 = 1300 kPa
= 1300 kPa
 =
=
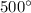
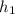 = 793kJ/K
= 793kJ/K
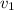 =
=

and also at
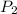 = 100 kPa
= 100 kPa
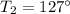
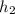 = 401 KJ/K
= 401 KJ/K
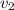 =
=
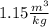
a) Mass flow rate is given by:
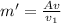
Now,
 = 46.51 kg/s
= 46.51 kg/s
b) for the power produced by turbine,
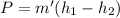
 = 18.231 MW
= 18.231 MW