Answer:
The probability that this whole shipment will be accepted is 0.8382. Almost all such shipments be accepted as the probability of accepting is higher.
Explanation:
Consider the provided information.
The probability for accepting the whole batch if there is only one or none that doesn't meet the required specifications.
Aspirin tablets actually has a 2% rate of defects. Thus, the rate of aspirin tablets are not defected 98%.
Which can be written as:
P(x=0 or x=1)
P(no defects out of 36)=
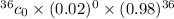
P(no defects out of 36)=

P(one defects out of 36)=
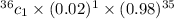
P(one defects out of 36)=
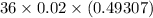
P(one defects out of 36)=
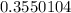
The probability that the whole shipment will accepted is the sum of the individual probabilities which is:
0.4832+0.3550=0.8382
Hence, the probability that this whole shipment will be accepted is 0.8382. Almost all such shipments be accepted as the probability of accepting is higher.