Question

How many ways can four numbers be drawn from a group of ten numbers if the order does not matter?

Answer 1

210 ways

Explanation:

Simply put in combinations and permutations,

ORDER MATTERS >> PERMUTATION

ORDER DOESNT MATTER >> COMBINATION

Formula for Permutation is
`P(n,r)=(n!)/((n-r)!)`

Formula for Combination is
`C(n,r)=(n!)/((n-r)!r!)`

These means taking r objects from a group of n

Also x! means x(x-1)(x-2)... (ex: 4! = 4 * 3 * 2 * 1)

Now, from the question, we have "order doesn't matter" so we have combination with n = 10 and r = 4.

Let's put the numbers into formula and find the answer:

`C(n,r)=(n!)/((n-r)!r!)\\C(10,4)=(10!)/((10-4)!4!)\\=(10!)/(6!4!)\\=(10*9*8*7*6!)/(6!4!)\\=(10*9*8*7)/(4*3*2*1)\\=210`

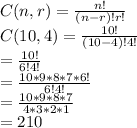
So, the answer is 210