Question

You’re inside a metal building that blocks radio waves, but you’re trying to make a call with your cell phone, which broadcasts at a frequency of 950 MHz. Down the hall from you is a narrow window measuring 35 cm wide. What’s the horizontal angular width of the beam (i.e., the angle between the first minima) from your phone as it emerges from the window?

Answer 1

θ= 128.896°

Step-by-step explanation:

In the Given question

f= 950 MHz

width of slit =35 cm = 0.35m

the expression to calculate angular width

`sin(\theta)/(2)=(\lambda )/(width of slit)`

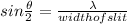
wavelength is

`\lambda =(c)/(f)`

`\lambda =(3* 10^8)/(950*10^6)`

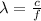
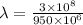
λ= 0.315 m

therefore angular width

`sin(\theta)/(2)=(0.315 )/(0.35)`

`sin(\theta)/(2)= 0.9022`

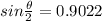
on further solving we get

θ= 2*64.448

θ= 128.896°

hence the horizontal angular width θ= 128.896°