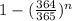Question

A company with n employees publishes an internal calendar, where each day lists the employees having a birthday that day. What is the probability there is at least one day in a year when nobody has a birthday?

Answer 1

Answer:
`1-((364)/(365))^n`

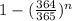
Explanation:

Binomial probability formula :-

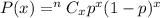`P(x)=^nC_xp^x(1-p)^x`, where P(x) is the probability of getting success in x trials, n is the total number of trials and p is the probability of getting success in each trial.

We assume that the total number of days in a particular year are 365.

Then , the probability for each employee to have birthday on a certain day :

`p=(1)/(365)`

Given : The number of employee in the company = n

Then, the probability there is at least one day in a year when nobody has a birthday is given by :-

`P(x\geq1)=1-P(x<1)\\\\1-P(0)\\\\=1-(^nC_0((1)/(365))^0(1-(1)/(365))^n)\\\\=1-(1)((364)/(365))^n\ \ \ \ \ \ [\text{since}\ ^nC_0=1]\\\\=1-((364)/(365))^n`

Hence, the probability there is at least one day in a year when nobody has a birthday =
`1-((364)/(365))^n`