Answer:
a)

b)
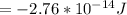
c)
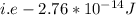
d)= 0 and the direction of motion is equal to zero
Step-by-step explanation:
a) compton shift
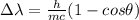


b) the new wavelength
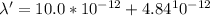


![=hc[(1)/(\lambda')-(1)/(\lambda)]](https://img.qammunity.org/2020/formulas/physics/high-school/t27ponpl3tix0w2h7xxpx0u3hkb2o3wx7x.png)
![\Delta E = 6.626*10^(-34)*(3*10^8)[(1)/(14.84*10^(-12))-(1)/(4.8*10^(-12))]](https://img.qammunity.org/2020/formulas/physics/high-school/biwtep80xno8tqkz7erm39b833wicc5h7i.png)
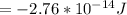
C)By conservation of energy, the kinetic energy of recoiling electron is equal to the magnitude of energy between the photon energy
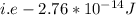
d) the angle between the positive direction of motion

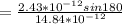
= 0
the direction of motion is equal to zero.