Question

A Carnot engine whose low-temperature reservoir is at 19.5°C has an efficiency of 23.0%. By how much should the Celsius temperature of the high-temperature reservoir be increased to increase the efficiency to 64.1%?

Answer 1

434.3727 °C

Step-by-step explanation:

Given :

The low temperature reservoir, TL = 19.5 °C

The conversion of T( °C) to T(K) is shown below:

T(K) = T( °C) + 273.15

So,

TL = (19.5 + 273.15) K = 292.65 K

Given: E₁ = 23.0 %

Let the temperature of the gas is , TH₁ = x K

The engine's efficiency of a Carnot engine is:

`Carnot's\ Efficiency=\frac {T_H-T_L}{T_H}* 100 \%`

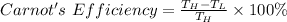
So,

`23.0 \%=\frac {(x)-292.15}{x}* 100 \%`

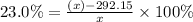
x = 379.4156 K

Now,

Given: E₂ = 64.1 %

Let the temperature of the gas is , TH₂ = y K

The engine's efficiency of a Carnot engine is:

`Carnot's\ Efficiency=\frac {T_H-T_L}{T_H}* 100 \%`

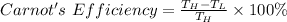
So,

`64.1 \%=\frac {(y)-292.15}{y}* 100 \%`

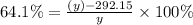
y = 813.7883 K

Also,

The conversion of T(K) to T( °C)is shown below:

T( °C) = T(K) - 273.15

x = 379.4156 K = 106.2656 °C

y = 813.7883 K = 540.6383 °C

The temperature that must be increased = 540.6383 °C - 106.2656 °C = 434.3727 °C