Answer:
A). σ = 3.823 x
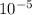
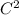 /N-
/N-
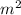
B).
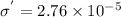 C/
C/
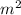
C).
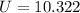 J
J
Step-by-step explanation:
A). We know magnitude of charge per unit area for a conducting plate is given by
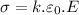
where, E is resultant electric field = 1.2 x
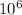 V/m
V/m
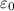 is permittivity of free space = 8.85 x
is permittivity of free space = 8.85 x
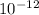
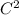 /N-
/N-
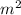
k is dielectric constant = 3.6
∴
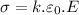
= 3.6 x 8.85 x
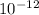 x 1.2 x
x 1.2 x
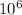
= 3.823 x
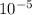
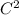 /N-
/N-
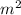
B).Now we know that the magnitude of charge per unit area on the surface of the dielectric plate is given by
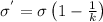
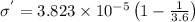
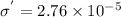 C/
C/
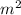
C).
Area of the plate, A = 2.5
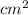
= 2.5 x
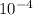
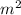
diameter of the plate, d = 1.8 mm
= 1800 m
∴ Total energy stored in the capacitor
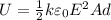
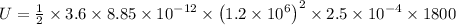
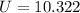 J
J