Question

As a fuel saving measure, commercial jets cruise at an altitude of about 10 km. While cruising at an altitude of 10 km, a small leak occurs in one of the window seals in the passenger compartment of an Airbus. Within the passenger compartment, the pressure and temperature are, respectively, 1.05 atm and 20°C and the pressure outside the craft is 0.274 atm. Model the air as an ideal fluid to find the speed (in m/s) of the stream of air flowing through the leak. (Assume the density of air to be 1.20 kg/m3.)

Answer 1

`v_o` = 357.26 m/s

Step-by-step explanation:

Given:

first convert both pressures to pascals

Outside pressure = 0.294 atm = 0.294 × 101300 = 29782.2 Pascals

Inside pressure = 1.05 atm = 1.05 × 101300 = 106365 Pascals

Now, using the Bernoulli's equation

, we have

`P_i + (1)/(2) \rho v_i^2=P_o + (1)/(2) \rho v_o^2`

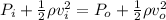
where

P is the pressure

v is the velocity

ρ is the density

i denotes the inside

o denotes the outside

the speed inside is approximately zero,thus

`106365 + (1)/(2) *1.20* 0^2=29782.2 + (1)/(2) *1.20* v_o^2`

`76582.8=(1)/(2) *1.20* v_o^2`

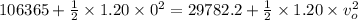
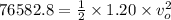
or

`v_o` = 357.26 m/s