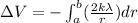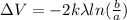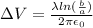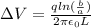Question

Two coaxial conducting cylindrical shells have equal and opposite charges. The inner shell has charge +q and an outer radius a, and the outer shell has charge -q and an inner radius b. The length of each cylindrical shell is L, and L is very long compared with b. Find the potential difference Va − Vb between the shells. (Use any variable or symbol stated above along with the following as necessary: k for the Coulomb's constant.)

Answer 1

`\Delta V = (q ln((b)/(a)))/(2\pi \epsilon_0 L)`

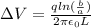
Step-by-step explanation:

As we know that the charge per unit length of the long cylinder is given as

`\lambda = (q)/(L)`

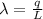
here we know that the electric field between two cylinders is given by

`E = (2k\lambda)/(r)`

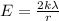
now we know that electric potential and electric field is related to each other as

`\Delta V = - \int E.dr`

`\Delta V = -\int_a^b ((2k\lambda)/(r))dr`

`\Delta V = -2k \lambda ln((b)/(a))`

`\Delta V = (\lambda ln((b)/(a)))/(2\pi \epsilon_0)`

`\Delta V = (q ln((b)/(a)))/(2\pi \epsilon_0 L)`