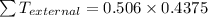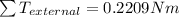Answer:
1)
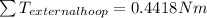
2)
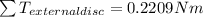
Step-by-step explanation:
Using the second equation of angular motion we have
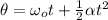
Since the wheels start from rest we ahve
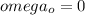
Applying the given values in the equation we have
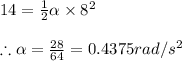
Now by newton's second law of motion in angular motion we have
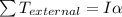
1) For Hoop We have
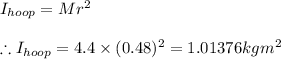
Thus
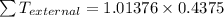
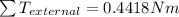
2)For disc We have
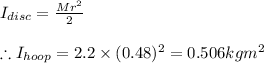
Thus