Question

A solid sphere rolls down an inclined plane without slipping. If the center of mass of the sphere has a linear acceleration of 1.21 m/s^2, what is the angle of the incline to the horizontal?

Answer 1

angle of inclination to the horizontal is 9.95°

Explanation:

Let the angle of inclination be θ

We know acceleration , a = 1.21 m/
`s^(2)`

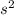
Now using effective mass concept, we get

`a = (m.g.sin\theta )/((m+l)/(r^(2)))`

`a = (m.g.sin\theta )/((m+0.4.m.r^(2))/(r^(2)))`

`a = (m.g.sin\theta.r^(2) )/(m(1+0.4r^(2)))`

`a = (m.g.sin\theta )/(1.4m)`

`1.21= (9.81sin\theta )/(1.4)`

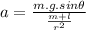
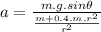
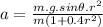
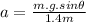
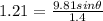
Therefore, solving for θ, we get

θ = 9.95°

Therefore, angle of inclination to the horizontal is 9.95°