Answer:
The correct option is 2.
Explanation:
Given information: A(4, –7), B(4, –2), C(0, –2), D(0, –7).
Distance formula:
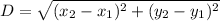
Using distance formula we get
Length of sides are
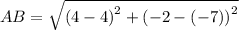
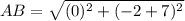
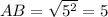
Similarly,
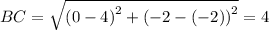
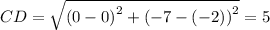
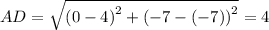
Length of diagonals are
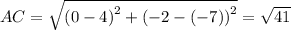
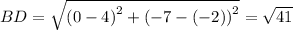
It figure ABCD,
1. AB and CD are opposite sides.
2. BC and AD are opposite sides.
3. AC and BD are diagonals.
From the above calculations it is clear that opposite sides are congruent, and diagonals are congruent. So, the figure ABCD is a rectangle.
Therefore the correct option is 2.