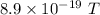Answer:
The magnitude of the magnetic field is
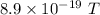
Step-by-step explanation:
Given that,
Electric field = 100 V/m
Radius = 4.0 cm
Electric field increase at a rate = 10 V/ms
Radial distance = 10.0 cm
We need to calculate the magnetic field
Using Gauss's law
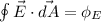
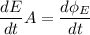
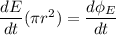
We need to calculate the
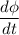
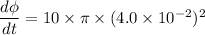
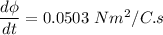
According to Ampere Maxwell law
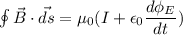
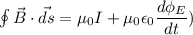
Electric field is zero inside the circle.
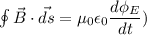
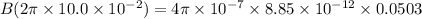
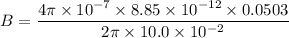

Hence, The magnitude of the magnetic field is