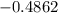Question

The mean pulse rate​ (in beats per​ minute) of adult males is equal to 69 bpm. For a random sample of 166 adult​ males, the mean pulse rate is 68.6 bpm and the standard deviation is 10.6 bpm. Find the value of the test statistic.

Answer 1

Answer:
`-0.4862`

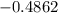
Step-by-step explanation:

Given : The mean pulse rate​ (in beats per​ minute) of adult males
`\mu=69\text{ bpm}`

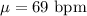
For sample : Size =
`n=166`

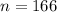
Mean :
`\overline{x}=68.6\text{ ppm}`

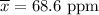
Standard deviation :
`\sigma=10.6\text{ bpm}`

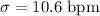
We assume that its a normal distribution , since the sample size is large (>30) then test applied here is z-test .

The formula to calculate the z-statistic is given by :-

`z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}`

`\Rightarrow\ z=(68.6-69)/((10.6)/(√(166)))=-0.486192404782\approx-0.4862`

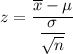
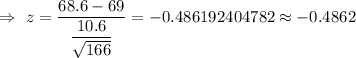
Hence, the value of the test statistic =
`-0.4862`