Question

The current density across a cylindrical conductor of radius R varies in magnitude according to the equation J = J0r/R where r is the distance from the central axis. Thus, the current density is a maximum J0 at the cylinder's surface and decreases linearly to zero at the axis. Calculate the current in terms of J0 and the conductor's cross-sectional area A = πR2 .

Answer 1

The current in the wire can be calculated using the current density and the cross-sectional area. In this case, the current is equal to CR⁴π, where C is a constant and R is the radius of the wire.

Step-by-step explanation:

The current in the cylindrical wire can be calculated by finding the total charge passing through a given cross-sectional area in the wire. The current is equal to the product of the current density and the cross-sectional area. In this case, the current density is given by J(r) = Cr² and the total cross-sectional area of the wire is A = πR². Therefore, the current outside the wire can be calculated as:

I = J(R)A = CR²πR² = CπR⁴

where I is the current just outside the wire, J(R) is the current density at the wire's surface, and R is the radius of the wire.

Answer 2

The total current is defined as the current density integrated over the cross-sectional area:

I = ∫JdA

I = total current, J = current density, dA = area element

We already have I as a given quantity:

J = (J₀/R)r

We need to find dA in terms of another variable so we can actually calculate the integral:

A = πr²

Differentiate both sides with respect to r:

dA/dr = 2πr

dA = 2πrdr

The conductor has a radius R, so set the integration bounds to [0, R]. Set the integrand to (2πJ₀/R)
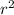`r^(2)` with r being the variable of integration.

I = (2πJ₀/3R)
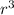`r^(3)` evaluated between r = 0 and r = R

I = (2πJ₀/3R)
`R^(3)`

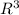
I = (2πJ₀/3)
`R^(2)`

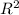
I = 2π
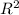`R^(2)`J₀/3

Substitute π
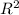`R^(2)` with area A:

I = 2AJ₀/3