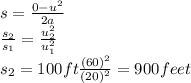Question

Assume you are driving 20 mph on a straight road. Also, assume that at a speed of 20 miles per hour, it takes 100 feet to stop. If you were to increase your speed to 60 miles per hour, your stopping distance is now:

Answer 1

900 feet

Step-by-step explanation:

Initial Speed, u₁ = 20 mph

Stopping distance, s₁ = 100 feet

Initial Speed, u₂ = 60 mph

Then, the stopping distance can be calculated using the third equation of motion:

`s=(v^2-u^2)/(2a)`

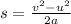
There would be same acceleration and final velocity would be zero (v=0).

`s=(0-u^2)/(2a)\\ (s_2)/(s_1)=(u_2^2)/(u_1^2)\\s_2= 100 ft((60)^2)/((20)^2) =900 feet`

Answer 2

Answer:900 feet

Step-by-step explanation:

Given

Velocity
`\left ( V_1\right )=20 mph\approx 29.334 ft/s`

it take 100 feet to stop

Using Equation of motion

`v^2-u^2=2as`

where

v,u=Final and initial velocity

a=acceleration

s=distance moved

`0-\left ( 29.334\right )^2=2\left (-a\right )\left ( 100\right )`

`a=(29.334^2)/(2* 100)=4.302 ft/s^2`

When velocity is 60 mph
`\approx 88.002 ft/s`

`v^2-u^2=2as`

`0-\left ( 88.002\right )^2=2\left ( -4.302\right )\left ( s\right )`

s=900.08 feet