Question

The radioactive element​ carbon-14 has a​ half-life of 5750 years. A scientist determined that the bones from a mastodon had lost 60.5​% of their​ carbon-14. How old were the bones at the time they were​ discovered?

Answer 1

7705.43 years.

Explanation:

Let us assume that initial amount of mastodon was 1.

We have been given that the radioactive element​ carbon-14 has a​ half-life of 5750 years. A scientist determined that the bones from a mastodon had lost 60.5​% of their​ carbon-14.

We will half life formula to solve our given problem.

`A=a\cdot ((1)/(2))^{(t)/(h)}`, where,

A= Final amount left after t years,

a = Initial amount,

t = time,

h = Half-life of substance.

Since the bones from a mastodon had lost 60.5​% of their​ carbon-14, so amount of carbon-14 left would be:

`1-60.5\%\rightarrow 1-(60.5)/(100)=1-0.605=0.395`

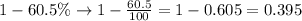
Upon substituting our given values in half'life formula, we will get:

`0.395=1\cdot ((1)/(2))^{(t)/(5750)}`

`0.395=(0.5)^{(t)/(5750)}`

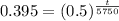
Upon taking natural log of both sides, we will get:

`\text{ln}(0.395)=\text{ln}((0.5)^{(t)/(5750)})`

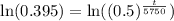
Using log property
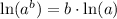`\text{ln}(a^b)=b\cdot \text{ln}(a)`, we will get:

`\text{ln}(0.395)=(t)/(5750)*\text{ln}(0.5)`

`\text{ln}(0.395)=\frac{t*\text{ln}(0.5)}{5750}`

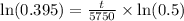
Now, we will divide both sides of our equation by
`\text{ln}(0.5)`.

`\frac{\text{ln}(0.395)}{\text{ln}(0.5)}=\frac{t*\text{ln}(0.5)}{5750* \text{ln}(0.5)}}`

`\frac{\text{ln}(0.395)}{\text{ln}(0.5)}=(t)/(5750)`

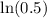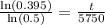
Switch sides:

`(t)/(5750)=\frac{\text{ln}(0.395)}{\text{ln}(0.5)}`

`(t)/(5750)=(-0.9288695)/(-0.693147180559)`

`(t)/(5750)=1.34007544159762`

`(t)/(5750)* 5750=1.34007544159762* 5750`

`t=7705.433789186`

`t\approx 7705.43`

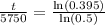
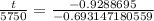
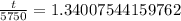
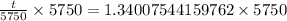
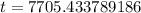
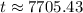
Therefore, the bones were approximately 7705.43 years old when they were discovered.