Question

Use long division to determine the quotient of the polynomials. (x3 – 7x – 6) ÷ (x – 4) Which of the following options best describes the relationship between the polynomial division and the remainder?

a. The quotient has a remainder of zero. Therefore, the divisor is a factor of the dividend.
b. The quotient has a remainder of 9. Therefore, the divisor is not a factor of the dividend.
c. The quotient has a remainder of 30. Therefore, the divisor is not factor of the dividend.
d. The quotient has a remainder of 36. Therefore, the divisor is a factor of the dividend.

Answer 1

The correct option is c.

Explanation:

The quotient of the polynomials is

`((x^3-7x-6))/(x-4)`

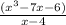
We need to find the remainder by using long division method.

The dividend of the given expression is

`Dividend=x^3-7x-6`

`Divisor=x-4`

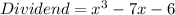
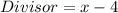
The long division method is shown below.

`((x^3-7x-6))/(x-4)=(x^2+4x+9)+(30)/(x-4)`

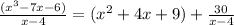
From the below attachment it is clear that the quotient has a remainder of 30. Therefore, the divisor is not factor of the dividend.

Therefore the correct option is c.