Question

An ant begins at the top of the pictured octahedron. If the ant takes two "steps", what is the probability it ends up at the bottom of the octahedron? Assume a "step" is a journey from one vertex to an adjacent vertex along an edge.

Answer 1

`(1)/(4)`

Step-by-step explanation:

Ant has 4 ways to go at first. No matter where it goes each way has 4 more ways. So to get to the bottom from 4 ways, there is only one way so, 1/4 is the answer

Answer 2

`P_(bottom)=(1)/(4)=0.25`

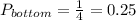
Step-by-step explanation:

Starting from the top, the ant can only take four different directions, all of them going down, every direction has a probability of 1/4. For the second step, regardless of what direction the ant walked, it has 4 directions: going back (or up), to the sides (left or right) and down. If the probability of the first step is 1/4 for each direction and once the ant has moved one step, there are 4 directions with the same probability (1/4 again), the probability of taking a specific path is the multiplication of the probability of these two steps:

`P_(2steps)=(1)/(4)*(1)/(4)=(1)/(16)`

There are only 4 roads that can take the ant to the bottom in 2 steps, each road with a probability of 1/16, adding the probability of these 4 roads:

`P_(bottom)=(1)/(16)+(1)/(16)+(1)/(16)+(1)/(16)=(4)/(16)=(1)/(4)`

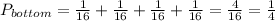
The probability of the ant ending up at the bottom is
`(1)/(4)` or 0.25.