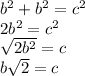Question

A RIGHT triangle has three sides: a, b, c such that a=b and LaTeX: a^2\:+\:b^2\:=\:c^2 a 2 + b 2 = c 2 What is the ratio of the longest side to the shortest? HINT:Sketch triangle NOTE: Angle A + Angle B = Angle C & Angle A= Angle B

Answer 1

`c=b√(2)`

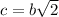
Explanation:

Refer to the attached image.

A right triangle is considered so when one of its corners are 90°.

If sides a and b are equal in length, then the corners across from them are equal in size as well.

The only way for this to be possible is if both corners A and B(opposite of sides a and b) are 45°.

Pythagorean theorem

This theorem states that the square of a right triangle's long side is equal to the sum of the squares of the shorter sides.

In this case:

`a^(2) +b^(2) =c^(2)`

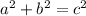
but since:

`a=b`

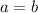
the equation can be solved by replacing a with b in the equation:

`b^(2) +b^(2) =c^(2) \\2b^(2)=c^(2) \\\sqrt{2b^(2) } = c\\b√(2) =c`