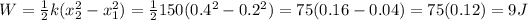Answer:
a. k=150N/m, b.W=0.75J,c. W=12J, d.W=9J
Step-by-step explanation:
a. The Hooke's Law states
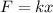 , where
, where
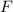 is the force,
is the force,
 the spring constant and
the spring constant and
 the displacement, Knowing the force and the displacement you can find
the displacement, Knowing the force and the displacement you can find
 :
:
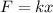
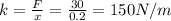
b. The work done by a force
 that moves along a displacement
that moves along a displacement
 is:
is:
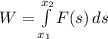
Then
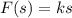 (Hooke's Law)
(Hooke's Law)

Work needed to go from
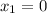 to
to
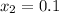
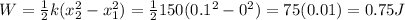
c. Work needed to go from
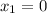 to
to

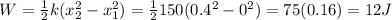
d. Work needed to go from
 to
to