Question

Use the Trapezoidal Rule, the Midpoint Rule, and Simpson's Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) 4 e2√t sin(2t) dt, n = 8 0

Answer 1

It looks like the integral could be

`\displaystyle\int_0^4\underbrace{e^(2\sqrt t)\sin(2t)}_(f(t))\,\mathrm dt`

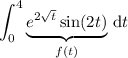
to be approximated by the three listed rules with
`n=8`.

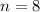Splitting up the interval of integration into 8 subintervals gives us the partition,

[0, 1/2], [1/2, 1], [1, 3/2], ..., [7/2, 4]

where the left and right endpoints, respectively, are given by the sequences

`\ell_i=\frac{i-1}2`

`r_i=\frac i2`

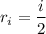
where
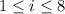`1\le i\le8`. The midpoints of each subinterval are given by

`m_i=\frac{\ell_i+r_i}2=\frac{\frac{i-1}2+\frac i2}2=\frac{2i-1}4`

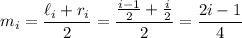
Each subinterval has length

`\Delta t_i=r_i-\ell_i=\frac i2-\frac{i-1}2=\frac12`

• Trapezoidal rule:

`\displaystyle\sum_(i=1)^8\frac{f(\ell_i)+f(r_i)}2\Delta t_i\approx11.070970`

• Midpoint rule:

`\displaystyle\sum_(i=1)^8f(m_i)\Delta t_i\approx10.767065`

• Simpson's rule:

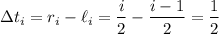
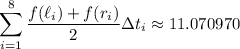
First we interpolate
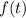`f(t)` over each subinterval with its own quadratic polynomial, given by

`p_i(t)=f(\ell_i)((t-m_i)(t-r_i))/((\ell_i-m_i)(\ell_i-r_i))+f(m_i)((t-\ell_i)(t-r_i))/((m_i-\ell_i)(m_i-r_i))+f(r_i)((t-\ell_i)(t-m_i))/((r_i-\ell_i)(r_i-m_i))`

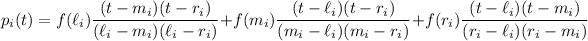
The integral is then approximately equal to

`\displaystyle\sum_(i=1)^8\int_(\ell_i)^(r_i)p_i(t)\,\mathrm dt`

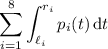
It turns out that

`\displaystyle\int_(\ell_i)^(r_i)p_i(t)\,\mathrm dt=\frac{r_i-\ell_i}6(f(\ell_i)+4f(m_i)+f(r_i))`

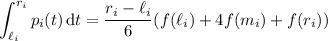
so the integral we want to approximate is about

`\displaystyle\sum_(i=1)^8\frac{r_i-\ell_i}6(f(\ell_i)+4f(m_i)+f(r_i))\approx10.868366`

Compare these results to the actual value of the integral, which is about 10.873071.