Answer:
(a) 1.2703×10⁻⁷ m
(b) 4.7636×10⁻⁸ m
(c) 2.5406×10⁻⁸ m
Step-by-step explanation:
Given:
Width of the infinite well, L = 340 pm = 340×10⁻¹² m.
The formula for energy of the electron in nth state is:

The expression for the difference in energy between the levels having quantum numbers n(initial) to n(final) is:
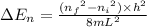
According to Planks theory:
E = hv
where, v is the frequency
Also,
Frequency×Wavelength = Speed of light
So,

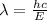
Also, using energy from above formula as:
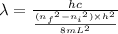

For longest wavelength ni = 1 and nf = 2
m= mass of the electron = 9.1 ×10⁻³¹kg
c = 3×10⁸m/s
h = 6.625×10⁻³⁴J.sec
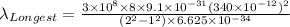
Longest wavelength = 1.2703×10⁻⁷ m
For second longest wavelength ni = 1 and nf = 3
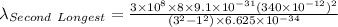
Second longest wavelength = 4.7636×10⁻⁸ m
For third longest wavelength ni = 1 and nf = 4
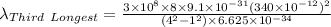
Third longest wavelength = 2.5406×10⁻⁸ m