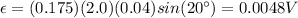Question

A square loop (length along one side = 20 cm) rotates in a constant magnetic field which has a magnitude of 2.0 T. At an instant when the angle between the field and the normal to the plane of the loop is equal to 20° and increasing at the rate of 10°/s, what is the magnitude of the induced emf in the loop?

Answer 1

0.0048 V

Step-by-step explanation:

The side of the coil is

L = 20 cm = 0.20 m

So the area is

`A=L^2 = (0.20)^2=0.04 m^2`

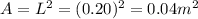
The magnetic flux through the coil at any instant t is

`\Phi = BA cos (\omega t)`

where

B = 2.0 T is the magnetic flux density

A is the area of the coil

`\omega` is the angular speed of the coil

t is the time

We know that the coil rotates at an angular speed of 10°/s, which converted into radians is

`\omega = (10 \cdot 2\pi)/(360)=0.175 rad/s`

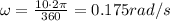
The magnitude of the induced emf in the loop is equal to the derivative of the magnetic flux, so:

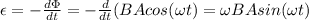`\epsilon =- (d\Phi)/(dt)=-(d)/(dt)(BA cos(\omega t) = \omega B A sin(\omega t)` (1)

We want to know the magnitude of the emf when the angle is
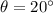`\theta=20^(\circ)`, so substituting this value of the angle into
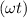`(\omega t)` in eq.(1), we find:

`\epsilon = (0.175)(2.0)(0.04) sin (20^(\circ))=0.0048 V`