Question

When
`2x^3-4x^2-5x-2` is divided by
`(x-1)(x+2)`, the remainder is
`(ax+b)`. This result may be expressed as the identity


`2x^3-4x^2-5x-2`≡
`(x-1)(x+2)Q(x)+ax+b`

where Q(x) is the quotient.


a) State the degree of Q(x).

b) By substituting suitable values of x, find a and b.

Answer 1

a) Q has degree 1.

b) a=5 while b=-14 ( I did this doing the way the problem suggested and I also did the problem using long division.)

Explanation:

a) Answer: Q has degree 1.

The left hand side's leading term is
`2x^3`.

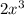If we expand (x-1)(x+2) we should see it's leading term is
`x(x)=x^2`

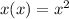
Since
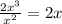`(2x^3)/(x^2)=2x` and 2x has degree 1, then our quotient must have degree 1.

Notes: I multiplied (x-1)(x+2) out in part b if you want to see what it looks like totally expanded.

b. Answer: a=5 while b=-14

You are given the following identity:

`2x^3-4x^2-5x-2=(x-1)(x+2)Q(x)+ax+b`

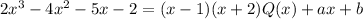
We want to be careful to choose values for x so that the expression for Q(x) doesn't matter.

If x=1, then
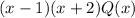`(x-1)(x+2)Q(x)` would be 0 since x-1 is zero at x=1.

That is plugging in 1 into term gives you:

`(1-1)(1+2)Q(1)`

`(0)(3)Q(1)`

`0Q(1)`

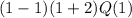
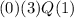
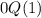
See what I mean the expression for Q doesn't matter because this result is 0 anyhow.

So let's plug in 1 into both sides:

`2(1)^3-4(1)^2-5(1)-2=(1-1)(1+2)Q(1)+a(1)+b`

`2-4-5-2=0Q(1)+a+b`

`-2-7=0+a+b`

`-9=a+b`

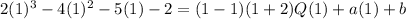
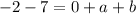
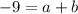
Now notice the factor x+2 in
`(x-1)(x+2)Q(x)`.

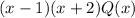x+2 is 0 when x=-2 since -2+2=0.

So we are going to plug in -2 into both sides:

`2(-2)^3-4(-2)^2-5(-2)-2=(-2-1)(-2+2)Q(-2)+a(-2)+b`

`2(-8)-4(4)+10-2=-3(0)Q(-2)-2a+b`

`-16-16+8=0-2a+b`

`-32+8=-2a+b`

`-24=-2a+b`

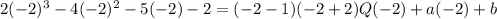
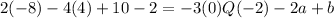
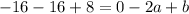
So the system to solve is:

a+b=-9

-2a+b=-24

--------------------Subtract the equations to eliminate b:

3a+0=15

3a =15

Divide both sides by 3:

3a/3=15/3

Simplify both sides:

1a=5

a=5

Using one of the equations we found along with a=5 we can not find b.

a+b=-9 with a=5

5+b=-9

Subtract 5 on both sides:

b=-9-5

b=-14

So a=5 while b=-14.

So ax+b is 5x-14.

We could do this another way not suggested by your problem but through long division:

First let's multiply (x-1)(x+2) out using foil.

First: x(x)=x^2

Outer: x(2)=2x

Inner: -1(x)=-x

Last: -1(2)=-2

-------------------Combine like terms:

x^2+x-2

Now let's do the division:

2x-6

----------------------------

x^2+x-2| 2x^3-4x^2-5x-2

-(2x^3+2x^2-4x)

-----------------------

-6x^2 - x -2

-(-6x^2-6x+12)

--------------------

5x-14

We see the remainder is 5x-14. This is what we also got doing as your problem suggested using values for x to plug in to find a and b.

Please let me know if something doesn't make sense to you. Have a good day.

Answer 2

a=5

b=-14

I'm not sure if this is what ur lookin for but this is supposed to be the answer