Answer:
The length of the median is 10, and the measure of the angle ∡A is 68°.
Explanation:
Let us start by the median. Recall that the median of a trapezoid is the segment that joins the midpoints of the non-parallel sides. In this case, the median will join the midpoints of the segments DA and CB. The length of the median of a trapezoid can be easily calculated by the formula
where
stands for the median,
for the larger of the parallel sides, and
for the shorter one. In this particular case
and
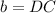. Thus,
.
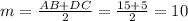Finally, recall that one of the main properties of isosceles trapezoid is that the angles adjacent to the parallel sides are equal. Then, as ∡B=68°, we conclude that ∡A is 68°.