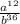For this case we must solve the following expression:
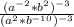
By definition of power properties we have to:
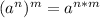
Rewriting we have to:
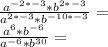
By definition we have to:
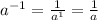
So:
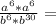
By definition of multiplication of powers of the same base, we place the same base and add the exponents:
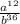
Answer: