Question

what are the x-coordinates for the maximum points in the function f(x) = 4 cos(2x- pi) from x = 0 to x= 2 pi?

Answer 1

`(\pi )/(2)` and
`(3\pi )/(2)`

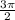
Explanation:

To find the max points we need to take the derivative of the function and then find the critical values.

First we take the derivative:

`f(x) = 4cos(2x-\pi )\\f'(x)=-4sin(2x-\pi )(2)\\f'(x)=-8sin(2x-\pi )\\`

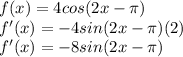
Now we need to find when f'(x)=0 to find the critical values.

`0=-8sin(2x-\pi )\\0=sin(2x-\pi )\\sin^(-1)0=2x-\pi \\0=2x-\pi \\\pi =2x\\(\pi )/(2) =x`

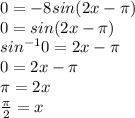
The critical values will be

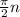`(\pi )/(2) n` for any integer n

between 0 and 2 pi, the critical values will be

`0, (\pi )/(2) ,\pi ,(3\pi )/(2),2\pi`

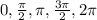
We can determine if these are minimums or maximums by using the second derivative test.

So we need to take the second derivative;

`f'(x)=-8sin(2x-\pi )\\f''(x) = -8cos(2x-\pi )(2)\\f''(x)=-16cos(2x-\pi)`

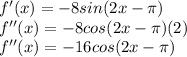
We need to see if the second derivative is positive or negative to determine if it is a max or min.

`f''(0) = 16\\f''((\pi)/(2))=-16\\f''(\pi )=16\\f''((2\pi)/(3)) = -16\\`

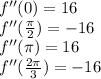
Since the second derivative is negative at

`(\pi )/(2)` and
`(3\pi )/(2)`

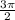
we know both of those are the x-values of maximums.