Answer:
Part 1) In the procedure
Part 2) There are 4 points of intersection (see the procedure)
Part 3) The answer in the procedure
Explanation:
we have
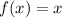 -----> linear function
-----> linear function
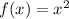 ----> quadratic function
----> quadratic function
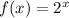 ----> exponential function
----> exponential function
Part 1) Which functions intersect?
using a graphing tool
we have that
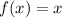 intersect with
intersect with
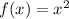
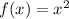 intersect with
intersect with
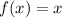 and
and
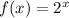
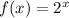 intersect with
intersect with
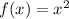
see the attached figure
Part 2) How many points of intersection are there?
In total there are 4 points of intersection
so
Between
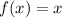 and
and
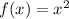
there are 2 points -----> (0,0) and (1,1)
Between
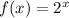 and
and
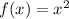
there are 2 points -----> (-0.77,0.59) and (2,4)
Part 3) What does a point of intersection mean?
we know that
A point of intersection between two functions means a common solution for both functions.
so
Example 1
The point (0,0) is a point of intersection between
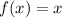 and
and
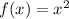
For x=0
Find the value of both functions
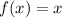 ----->
----->
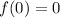
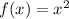 ---->
---->
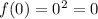
Both functions have the same value
Example 2
The point (2,4) is a point of intersection between
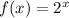 and
and
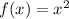
For x=2
Find the value of both functions
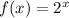 ----->
----->
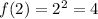
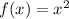 ---->
---->
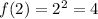
Both functions have the same value