Answer:
12
Explanation:
We are given that two equations

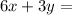
We have to find the value in the blank space when we place that value then system of equations have infinitely many solutions
Equation I can be written as
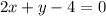
Let a be the value that placed in blank space and system have infinitely many solutions
Then
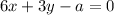
We know that condition of infinite solutions

Substitute the values then we get

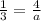
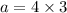
a=12
Hence, when we placed 12 in the box then system of equations would have infinitely many solutions .
'