Question

Write the equation of an ellipse with vertices at (7, 0) and (-7, 0) and co-vertices at (0, 1) and (0, -1).

Answer 1

`((x)^(2))/(49)+((y)^(2))/(1)=1`

Explanation:

In this problem we have a horizontal ellipse, because the major axis is the x-axis

The equation of a horizontal ellipse is equal to

`((x-h)^(2))/(a^(2))+((y-k)^(2))/(b^(2)) =1`

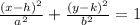
where

(h,k) is the center of the ellipse

a and b are the respective vertices distances from center

we have

vertices at (7, 0) and (-7, 0)

co-vertices at (0, 1) and (0, -1)

so

The center is the origin (0.0) (The center is the midpoint of the vertices)

a=7

b=1

substitute

`((x-0)^(2))/(7^(2))+((y-0)^(2))/(1^(2))=1`

`((x)^(2))/(49)+((y)^(2))/(1)=1`