Question

A heat engine operates between two reservoirs at 300K. During each cycle, it absorbs 200 calories from the high temperature reservoir. Calculate:

(a) The maximum efficiency of the system
(b) The maximum works the engine can perform in each cycle

Answer 1

(a) Zero

The maximum efficiency (Carnot efficiency) of a heat engine is given by

`\eta=1-(T_C)/(T_H)`

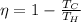
where

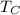`T_C` is the low-temperature reservoir

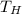`T_H` is the high-temperature reservoir

For the heat engine in the problem, we have:

`T_C = 300K`

`T_H = 300K`

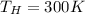
Therefore, the maximum efficiency is

`\eta=1-(300)/(300)=0`

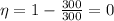
(b) Zero

The efficiency of a heat engine can also be rewritten as

`\eta = (W)/(Q_H)`

where

W is the work performed by the engine

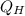`Q_H` is the heat absorbed from the high-temperature reservoir

In this problem, we know

`\eta=0`

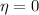
Therefore, since the term
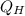`Q_H` cannot be equal to infinity, the numerator of the fraction must be zero as well, which means

W = 0

So the engine cannot perform any work.