Question

The graphs below have the same shape. what is the equation of the graph of g(x)?

Answer 1

D. g(x) = (x+4)²

Explanation:

From the graph of g(x), we can see that if we plug in -4 to g, or in the proper notation, g(-4), it should equal 0. It should do the same with the equations. The only equation that equals 0 when -4 is plugged in is D. Therefore, your answer is D.

Answer 2

`D. g(x)=(x+4)^(2)`

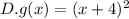
Explanation:

As you can see in the graph, the point where the parabola starts is (-4,0), this graph is already in Y form, so we know that at some point in the graph, Y would be 0 and x would have to be -4, so we just have to evaluate the options for 0.

`g(x)=(x+4)^(2)\\0=(x+4)^(2)\\0=x+4\\x=-4`

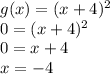
As D is the only option that is evaluated for 0 and as a result gives -4, that is the answer for the equation of the graph.