Question

Select the true statement about triangle ABC. Need answer asap

Answer 1

B. sinC= cosA
Remember SohCahToa.
The sine is equal to opposite/hypotenuse and cosine is equal to adjacent over hypotenuse.
The sine of C is 12/13 and the cosine of A is 12/13.

Answer 2

Answer: The correct option is

(B)
`\sin C=\cos A.`

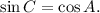
Step-by-step explanation: We are given to select the true statement about the triangle ABC shown in the figure.

From the figure, we note that

triangle ABC is right-angled at angle B, where hypotenuse, AC = 13, BC = 5 and AB = 12.

From the trigonometric ratios, we have

`\sin A=\frac{\textup{perpendicular}}{\textup{hypotenuse}}=(BC)/(AC)=(5)/(13),\\\\\\\cos A=\frac{\textup{base}}{\textup{hypotenuse}}=(AB)/(AC)=(12)/(13),\\\\\\\cos B=\frac{\textup{base}}{\textup{hypotenuse}}=(BC)/(AC)=(5)/(13),\\\\\\\sin C=\frac{\textup{perpendicular}}{\textup{hypotenuse}}=(AB)/(AC)=(12)/(13),\\\\\\\sin A=\frac{\textup{perpendicular}}{\textup{hypotenuse}}=(BC)/(AC)=(5)/(13),\\\\\\\tan A=\frac{\textup{perpendicular}}{\textup{base}}=(BC)/(AB)=(5)/(12).`

Therefore, we get

`\sin C=\cos A.`

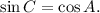
Thus, option (B) is CORRECT.