Question

Please can anyone help answer this question? It would be greatly appreciated!!! :)

Answer 1

The probability that point falls in the white area is 2/3 or 0.667

Explanation:

Consider the provided figure.

As we know there are 360 degrees in a circle.

The diameter divides the circle in two equal half 180° each.

The angle measure of white part in upper half is 180°-60°-60°=60°

The total angle measure of white part in the provided figure is: 180°+60°=240°

Now we need to find the probability that a random selected point falls in the white area

`Probability=\frac{\text{Number of favorable outcomes}}{\text{Total number of outcomes}}`

Substitute Number of favorable outcomes=240° and Total number of outcomes = 360° in the above formula.

`Probability=(240)/(360)`

`Probability=(2)/(3)\ \text{or}\ 0.667`

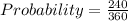
Hence, the probability that point falls in the white area is 2/3 or 0.667