Question

The lengths of human pregnancies are normally distributed with a mean of 268 days and a standard deviation of 15 days. What is the probability that a pregnancy last at least 300​ days? Round to four decimal places. A. 0.0164 B. 0.9834 C. 0.4834 D. 0.0179

Answer 1

Answer: A. 0.0164

Explanation:

Given : The lengths of human pregnancies are normally distributed with a mean
`\mu=268\text{ days}`

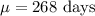
Standard deviation :
`\sigma=15\text{ days}`

Let X be the random variable that represents the length of pregnancy of a randomly selected human .

z-score :
`z=(X-\mu)/(\sigma)`

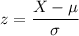
For X = 300

`z=(300-268)/(15)\approx2.13`

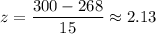
Now, the probability that a pregnancy last at least 300​ days will be :-

`P(X\geq300)=P(z\geq 2.1333)=1-P(z<2.1333)\\\\=1- 0.9835513=0.0164487\approx0.0164`

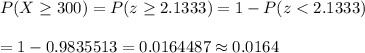
Hence, the probability that a pregnancy last at least 300​ days =0.0164