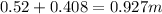Question

You’re standing in waist-deep water with your eyes 0.52 m m above the surface. A fish is swimming 0.65 m below the surface. Your line of sight to the fish makes a 45 ∘ angle with the water’s surface. Part A How far (horizontally) from you is the fish?

Answer 1

Required horizontal distance is 0.9279 meters

Step-by-step explanation:

The situation is represented in the attached figure

The horizontal distance can be seen to be equal to

`H=H_(1)+H_(2)`

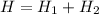
In the upper triangle we have

`tan(45^(o))=(0.52m)/(H_(1))\\\\\therefore 1=(0.52)/(H_(1))\\\\\therefore H_(1)=0.52m`

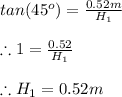
Now the angle
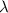`\lambda` can be calculated using Snell's law

By snell's Law we have

`\mu _(1)sin(\theta _(1))=\mu _(2)sin(\theta _(2))`

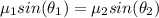
Since light comes from air thus
`\mu _(1)=1`

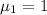
Light enter's the water thus we have
`\mu _(2)=1.33`

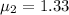
Applying values we calculate
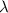`\lambda` as

`1* sin(45^(o))=1.33sin(\lambda _(r))\\\\\lambda _(r)=sin^(-1)((sin(45^(o)))/(1.33))\\\\\lambda _(r)=32.11^(o)`

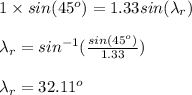
Now in the attached figure we have

`tan(90-\lambda _(r))=(0.65)/(H_(2))\\\\\therefore tan(90-32.11)=(0.65)/(H_(2))`

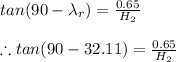
Solving for
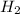`H_(2)` we get

`H_(2)=(0.65)/(tan(90-32.11))\\\\H_(2)=0.408m`

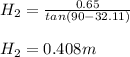
thus the required horizontal distance is
`0.52+0.408=0.927m`