Step-by-step explanation:
From first source, kinetic energy (
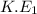 ) ejected is 1 eV and wavelength of light is
) ejected is 1 eV and wavelength of light is
 .
.
From second source, kinetic energy (
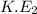 ) ejected is 4 eV and wavelength of light is
) ejected is 4 eV and wavelength of light is
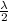 .
.
Relation between work function, wavelength, and kinetic energy is as follows.
K.E =

where, h = Plank's constant =
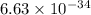 J.s
J.s
c = speed of light =
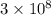 m/s
m/s
Also, it is known that 1 eV =
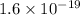 J
J
Therefore, substituting the values in the above formula as follows.
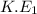 =
=

1 eV =
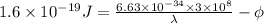
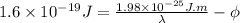 ........... (1)
........... (1)
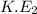 =
=

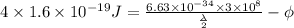
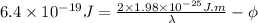 ........... (2)
........... (2)
Now, divide equation (2) by 2. Therefore, it will become

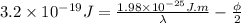 ......... (3)
......... (3)
Now, subtract equation (3) from equation (1), we get the following.

 =
=
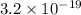
= 2 eV
Thus, we can conclude that work function of the metal is 2 eV.