Question

X-rays with an energy of 400 keV undergo Compton scattering with a target. If the scattered X-rays are detected at \theta = 30^{\circ}θ=30 ​∘ ​​ relative to the incident X-rays, what is the energy of the recoiling electron?

Answer 1

The energy of recoiling electron=192.44 keV

Step-by-step explanation:

Energy of x-ray
`E_o=400 keV`

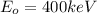
Web know that compton shift is

`\Delta \lambda =(h)/(m_eC(1-cos\theta))`

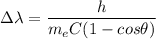
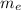`m_e` is the mass of electron and C is the velocity of sound.

Given that θ=30°

Now by putting the values

`\Delta \lambda =(6.63* 10^(-34))/(9.11* 10^(-31)* 3* 10^8(1-cos30))`

`\Delta \lambda =2.8* 10^(-3)nm`

`\Delta \lambda_o=(hc)/(E_o)`

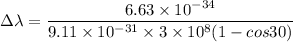
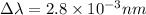
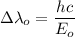
By putting the values

`\Delta \lambda_o=(6.63* 10^(-34)3* 10^8)/(400* 1.602* 10^(-16))`

`\Delta \lambda_o=3.31times 10^(-3)nm`

`\lambda =\Delta \lambda +\lambda _o`

`\lambda=2.8* 10^(-3)+3.31* 10^(-3)nm`

`\lambda=6.11`* 10^(-3)nm`

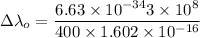
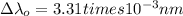
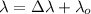
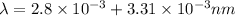
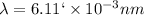
Energy
`E=(hC)/(\lambda )`

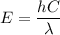
So
`E=(6.63* 10^(-34)* 3* 10^8)/(6.11* 10^(-12))`

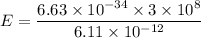
E=207.55 keV

The energy of recoiling electron=400-207.55 keV

The energy of recoiling electron=192.44 keV

Answer 2

37.91594 keV

Step-by-step explanation:

`E_i` = Incident energy = 400 keV

θ = 30°

h = Planck's constant = 4.135×10⁻¹⁵ eV s = 6.626×10⁻³⁴ J s

Incident photon wavelength

`\lambda_i=(hc)/(E_i)\\\Rightarrow \lambda_i=(4.135* 10^(-15)* 3* 10^8)/(400* 10^3)\\\Rightarrow \lambda_i=3.101* 10^(-12)\ m`

Difference in wavelength

`\Delta \lambda=(h)/(m_ec)(1-cos\theta)\\\Rightarrow \Delta \lambda=(6.626* 10^(-34))/(9.11* 10^(-31)* 3* 10^8)(1-cos30)\\\Rightarrow \Delta \lambda=3.248* 10^(-13)\ m`

`\lambda_f=\lambda_i+\Delta \lambda\\\Rightarrow \lambda_f=3.101* 10^(-12)+3.248* 10^(-13)\\\Rightarrow \lambda_f=3.426* 10^(-12)`

Final photon wavelength

`\lambda_f=(hc)/(\lambda_f)\\\Rightarrow E_f=(4.135* 10^(-15)* 3* 10^8)/(3.426* 10^(-12))\\\Rightarrow E_f=362084.06\ eV = 362.08406\ keV`

Energy of the recoiling electron

`\Delta E=E_i-E_f\\\Rightarrow \Delta E=400-362.08406=37.91594\ keV`

Energy of the recoiling electron is 37.91594 keV