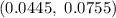Question

A Bernoulli random variable X has unknown success probability p. Using 100 independent samples of X, find a confidence interval estimate of p with confidence coefficient 0.99. If ????????100 = 0.06, what is our interval estimate

Answer 1

Answer:
`(0.0445,\ 0.0755)`

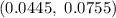
Explanation:

The confidence interval for the population proportion is given by :-

`p\pm z_(\alpha/2)\sqrt{(p(1-p))/(n)}`

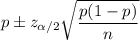
Given : A Bernoulli random variable X has unknown success probability p.

Sample size :
`n=100`

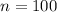
Unknown success probability :
`p=0.06`

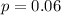
Significance level :
`\alpha=1-0.99=0.01`

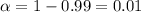
Critical value :
`z_(\alpha/2)=2.576`

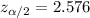
Now, the 99% confidence interval for true proportion will be :-

`0.06\pm(2.576)\sqrt{(0.06(0.06))/(100)}\\\\\approx0.06\pm(0.0155)\\\\=(0.06-0.0155,\ 0.06+0.0155)\\\\=(0.0445,\ 0.0755)`

Hence, the 99% confidence interval for true proportion=
`(0.0445,\ 0.0755)`