Question

In a sample of 200 men, 130 said they wore seatbelts. In a sample of 300 women, 140 said they wore seatbelts. Find a 95% confidence interval for the difference in proportion of men and women who wear seatbelts. g

Answer 1

The total number of men is 32. Of these men, 25 wore a watch. So, the number of men who didn’t wear a watch is 7, because 32 − 25 = 7.

Explanation:

Answer 2

Answer: (0.093,0.267)

Explanation:

The confidence interval for the difference in proportion is given by :-

`(p_1-p_2)\pm z_(\alpha/2)\sqrt{(p_1(1-p_1))/(n_1)+(p_2(1-p_2))/(n_2)}`

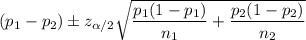
Given :
`n_1=200`;
`n_2=300`

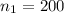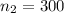
Proportion of men said they wore seatbelts =
`p_1=(130)/(200)=0.65`

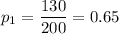
Proportion of women said they wore seatbelts =
`p_2=(140)/(300)\approx0.47`

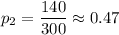
Significance level :
`\alpha=1-0.95=0.05`

Critical value :
`z_(\alpha/2)=z_(0.025)=1.96`

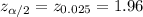
Now, the 95% confidence interval for the difference in proportion of men and women who wear seatbelts will be :-

`(0.65-0.47)\pm (1.96)\sqrt{(0.65(1-0.65))/(200)+(0.47(1-0.47))/(300)}\\\\\approx0.18\pm0.087\\\\=(0.093,0.267)`

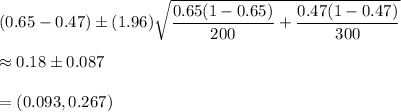
Hence, the 95% confidence interval for the difference in proportion of men and women who wear seatbelts = (0.093,0.267)