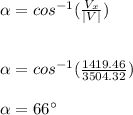Answer:
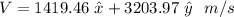
Or
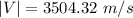 with
with
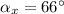
Step-by-step explanation:
We know that the initial speed is:
1350 m/s at a 25 degree angle
And the final position after 10.20 sec is:
23,500 m away in a 55 degree direction
In this problem we have:
Final position in x:
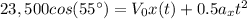
Where
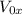 is the initial velocity in x
is the initial velocity in x
So:
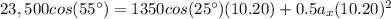
We solve for
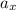
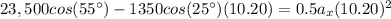
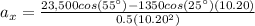
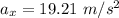
X component of velocity
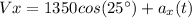
Where
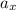 is the acceleration in the direction x
is the acceleration in the direction x
And
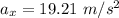
Therefore:
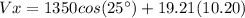
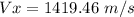
Final position in y:
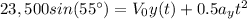
Where
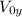 is the initial velocity in y
is the initial velocity in y
So:
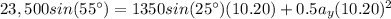
We solve for
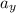
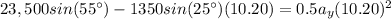
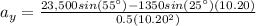
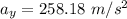
Y component of velocity
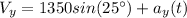
Where
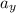 is the acceleration in the direction y
is the acceleration in the direction y
And
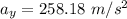
Therefore:
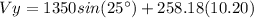
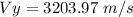
Note then that the final velocity V is a two component vector
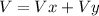
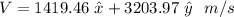
The magnitude of the final speed is:
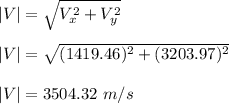
And the angle that forms with the x axis is: