Answer: (a) (602.95,705.37)
(b) 33
Explanation:
(a) Given : Sample size :

Sample mean :
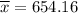
Standard deviation :
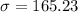
Significance level :

Critical value :
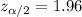
The confidence interval for population mean is given by :-
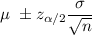
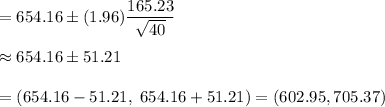
Hence, the 95% (two-sided) confidence interval for true average
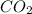 level in the population of all homes from which the sample was selected.
level in the population of all homes from which the sample was selected.
(b) Given : Standard deviation :
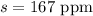
Margin of error :
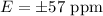
Significance level :

Critical value :
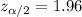
The formula to calculate the sample size is given by :-

Hence, the minimum required sample size would be 33.