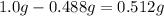Question

A compound distributes between benzene (solvent 1) and water (solvent 2) with a distribution coefficient, K = 2.7. If 1.0g of the compound were dissolved in 100mL of water, what weight of compound could be extracted by THREE sequential 10-mL portions of benzene?

Answer 1

Step-by-step explanation:

The given data is as follows.

Solvent 1 = benzene, Solvent 2 = water

`K_(p)` = 2.7,
`V_{S_(2)}` = 100 mL

`V_{S_(1)}` = 10 mL, weight of compound = 1 g

Extract = 3

Therefore, calculate the fraction remaining as follows.

`f_(n) = [1 + K_(p)(\frac{V_{S_(2)}}{V_{S_(1)}})]^(-n)`

=
`[1 + 2.7((100)/(10))]^(-3)`

=
`(28)^(-3)`

=
`4.55 * 10^(-5)`

Hence, weight of compound to be extracted = weight of compound - fraction remaining

= 1 -
`4.55 * 10^(-5)`

= 0.00001

or, =
`1 * 10^(-5)`

Thus, we can conclude that weight of compound that could be extracted is
`1 * 10^(-5)`.

Answer 2

It could be extracted 0.512 g of solute

Step-by-step explanation:

The equation that relates the
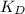`K_(D)` and the volumes of organic and aqueous phases is:

`q_(solute-aq) =(V_(aq) )/(K_(D)xV_(org) + V_(aq)  )`

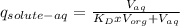
Where q_{solute-aq} refers to the fraction of solute remaining in the aqueous phase, V_{aq} is the aqueos phase volume, V_{org} is the organic phase volume and K_{D} is the partition coefficient of the solute in the solvents.

Moreover,for the three consecutive extractions of the same volume of organic phase we can write:

`q_(solute-aq) =((V_(aq) )/(K_(D)xV_(org) + V_(aq)  ))^( 3)`

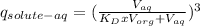
So, plugging the values given into the equation we get:

`q_(solute-aq) =((100 mL )/(2.7x10 mL + 100 mL  ))^( 3)`

`q_(solute-aq) =0.488`

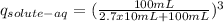
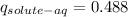
The result obtained indicates that a fraction of 0.488 of solute remains in the aqueous phase.

Taking in account that the fraction formula is:

`q_(solute-aq) = (mass- of- solute- aq)/(initial-mass- of -solute)`

`0.488= (mass- of- solute- aq)/(1.0 g)\\\\0.488 x 1.0 g= {mass- of- solute- aq}\\0.488 g= {mass- of- solute- aq}\\`

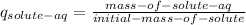
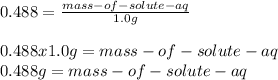
Finally we substract the solute in the aqueous phase form the initial to get the amount in the organic phase:

`1.0g - 0.488g = 0.512 g`